At the ecosystem level, carbon (CO2) is fixed through photosynthetic carbon metabolism, and then fixed carbon is used for growth and development of plants. Some of the fixed carbon will be lost through respiration. Inside a clear chamber, net carbon exchange (NCE) is defined as the carbon exchange between an ecosystem and the atmosphere, which is the photosynthesis uptake minus the total respiration, including above ground respiration and soil respiration. It is a key variable for understanding the carbon balance of an ecosystem. NCE can be readily measured with the eddy covariance method over a large uniform field or with the chamber-based method for short and small canopies. If no plants are present inside the clear chamber, then the measured NCE is the soil respiration.
For a clear chamber, the mass balance for CO2 inside the chamber would be (see equation 1‑12 for more information);
1‑23
where ρc is the air number density inside the chamber (mol m-3), S is the surface area inside the chamber (m2), and wc is the chamber air water vapor mole fraction (mol mol-1). Cc’ is chamber CO2 mole fraction corrected for water vapor dilution.
For soil CO2 flux fc:
1‑24
Where fc is soil CO2 flux (mol m-2s-1), and all other variables have the same definitions as described in the section for opaque chambers (see Deriving the flux equation: the model).
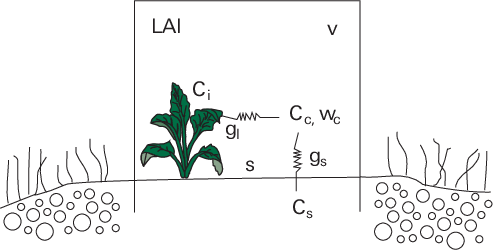
When you have living plants with leaf area index, (LAI, defined as the ratio of total one-sided leaf area inside the clear chamber to ground area), the CO2 uptake rate via photosynthesis (fp) would be:
1‑25
Where fp is the photosynthesis rate (mol m-2s-1), gl is the total leaf conductance (mol m-2s-1) including stomatal and leaf boundary layer conductance, Ci’ is intercellular CO2 mole fraction (mol mol-1), is Ci/Ca ratio. We assume α to be constant over a wide range of CO2 concentrations (around 0.6 for C3 species, and 0.3 for C4 species) (Wong et al., 1979; Morison, 1987; Xu and Hsiao, 2004).
where Rh is total above-ground biomass respiration. Rearranging equation 1‑26, we have
1‑27
Let and
Equation 1‑28 can be integrated to have
Let , we have
The following equation will be used to fit the time series of Cc’ (see earlier in this section for an explanation of the origin of t0)
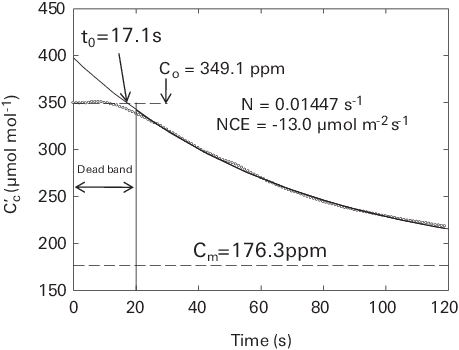
Equation 1‑28 is exactly the same as equation 1‑15 for opaque chambers. For the LI-8100A, we use a generic exponential equation to fit the time series of chamber CO2 concentration. For a clear chamber, when Cm’ < C0’, net carbon uptake is observed. When Cs’ > C0’ from fitted equation 1‑28, net carbon release is observed.
The net carbon exchange then can be estimated using equation 1‑12, with the information from the initial slope of the time series of Cc’ (equation 1‑29). Negative flux values will be reported for the cases of net carbon uptake and positive flux will be reported for the cases of net carbon release. Note that Cm represents the CO2 compensation point at which photosynthesis rate is equal to total respiration rate inside the chamber.
The above derivation involved some assumptions to be able to solve the differential equation 1‑29 analytically. Not all assumptions are valid for all cases. For example, we assume stomatal conductance is independent of air CO2 level, which clearly is not the case. The purpose of this exercise is to provide a general view on how the time series of chamber CO2 concentration behaves after the chamber is closed.
The considerations for setting up the configuration (dead band, observation length, observation count, Pre-purge) for the clear chamber measurement are the same as for other LI-COR opaque chambers (8100-101, -102, -103, -104).