Measuring the response time of blank media
Media chemistry will impact the "time to steady state" for measurements in the aquatic chamber. For many situations, the effect of media on the total response time will be larger than that of the instrument itself or the physiology being measured. As such, a rough characterization of the media-only response time is a good idea before attempting physiological measurements.
- Prepare the instrument for measurements.
- Set the flow rate to your normal working flow. 400 µmol s-1 is reasonable to use for this.
- Turn ON both the aquatic chamber pump and mixing fan.
- Set H2O_s to a value below dew point at the current ambient temperature. For typical room temperature measurements 20 mmol mol-1 is a good starting point.
- Set CO2_r to a value around that used for typical measurements. In the example here, CO2_r was set to 400 µmol mol-1.
- Set temperature to your normal working temperature. See Controlling temperature with a water bath.
- Load a volume of the media you will use for measurements into the aquatic chamber.
- We recommend a 15 mL volume. Be sure the media is at the nominal working temperature and includes all additions (i.e., carbonic anhydrase) that may be used during typical measures. In the example shown here, deionized water with no carbonic anhydrase was used.
- When the reported flux becomes stable, match the IRGAs.
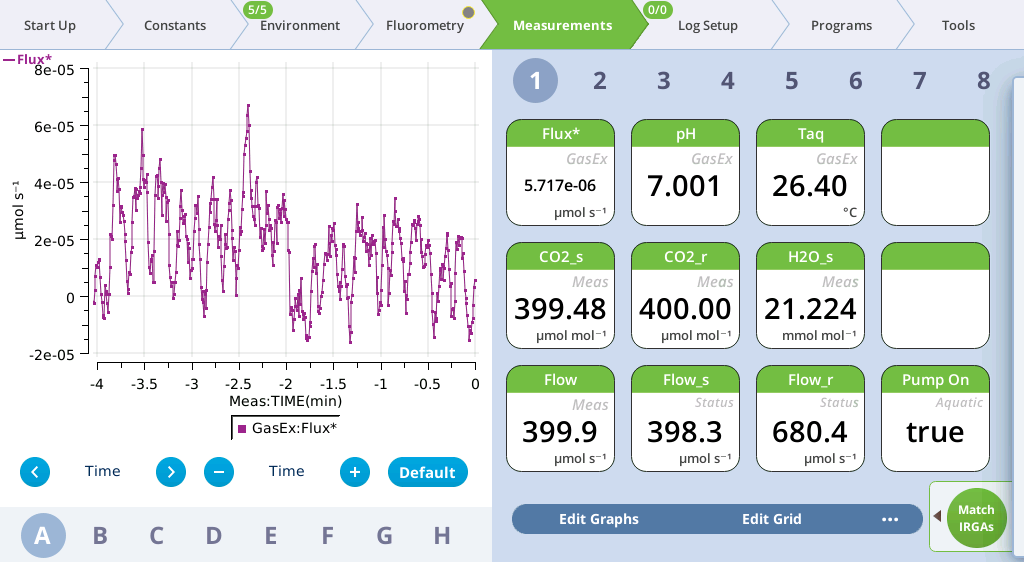
- The reported flux should go to zero (or very close to zero) after matching. If it doesn’t, the sample is not in equilibrium with the cuvette headspace. Wait a little longer before trying the match again.
- After matching at the current CO2_r, set CO2_r to some new value.
- Choose a concentration fairly far away from the starting concentration. In the example here, CO2_r was increased to 600 µmol mol-1.
- Note the time that you made the step change.
- If it takes longer than 16 minutes to reach steady state at the new concentration, you will need this time to estimate the time constant for the media. (16 minutes is the most time that can be displayed on the X-axis.)
- Watch graphs A and C.
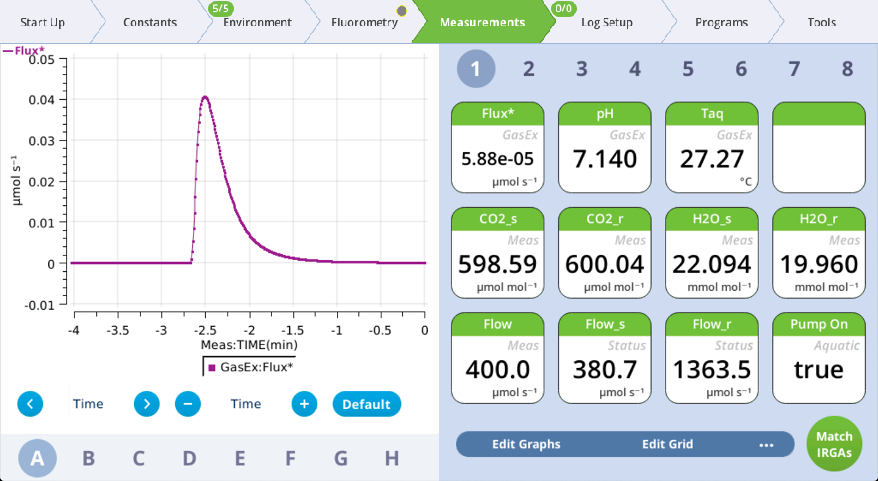
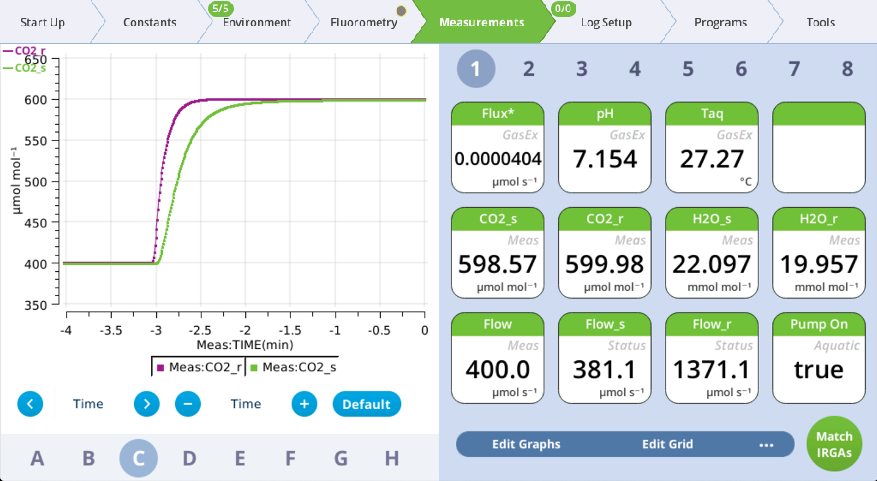
- Once the reported flux is constant again and CO2_r is constant at the new setpoint, note the time.
- The flux may not be zero at this point. Match offsets are a function of concentration and by changing the concentration, our previous match adjustment may no longer be valid. For real measurements, this detail matters a lot, but for this exercise, not so much. But if you want to be certain the media is equilibrated at the new concentration, match and ensure a flux of zero is reported.
- Compute the time constant: The difference between time noted in steps 7 and 5 divided by four gives a rough approximation of the time constant for the media.
- We use a divisor of four here to be little conservative. The time constant represents how long it takes to reach 63% of the response. So, four time constants is only 98% of the full change. In the example shown here, it took about 2.5 minutes to reach a constant flux, suggesting that the time constant in this example is around 40 seconds.
What do you do with this information? It is tempting to assume that this means that it will take 2.5 minutes at a minimum for all measurements in the example media. But that would be a misapplication of the concept.
Here we gave a 200 µmol mol-1 step change to the system and observed that after 2.5 minutes the difference in CO2_s and CO2_r was well less than 4 µmol mol-1 (the residual difference after getting 98% of the way through a 200 µmol mol-1 step change). If, by chance, we were characterizing a 10 µmol mol-1 step change, as might be seen when changing light levels during a photosynthesis irradiance experiment, the 98% mark would be 0.4 µmol mol-1. Depending on the magnitude of the fluxes being measured, that 0.4 µmol mol-1 difference may be important, or it might not. On a delta CO2 of 4 µmol mol-1, that is 10% and you may want to wait longer. On a delta of 40 µmol mol-1, it is 1% and you may not want to wait as long.
